三井情報は、材料開発の生産性向上に向けた研究開発に取り組んでいます。今回は、材料開発において効率的な物質の探索を実現するために有効な、「多目的最適化」の手法についてお話しします。
材料開発の重要なタスクの一つは、ターゲットとなる性能指標(e.g. 電気伝導率の最大化)を定めた上で、その指標を達成する物質を探索することです。複数の指標があると「あちら立てればこちらが立たぬ」、いわゆるトレードオフが生じることがあります。トレードオフがある場合、複数の指標を同時に達成する物質の探索が難しくなります。そこで有効となるのが多目的最適化ですが、まずはトレードオフについて身近な例を挙げて説明します。
身近にあるトレードオフ
世の中一般の事象にはトレードオフがつきものです。たとえば賃貸マンションにおいて、面積や築年数の似た複数の物件を比較すると、駅に近い便利な物件ほど賃料が高くなる傾向が見られます。駅の近くにもかかわらず他より賃料が安い物件というものは、なかなか見つかりません。賃貸マンションの物件における利便性の高さと賃料の安さは、互いに両立することができない、トレードオフの関係にあると言えます。トレードオフの関係がみられる例は、他にもあります。ソフトウェア開発において、機能を充実させることでユーザの満足度向上が期待できる一方で、リリースが遅れて開発費も増えるケース(*1)。自動車や航空機の設計において、強度・重量・空気抵抗など複数の相反する指標を満たす案を出す必要のあるケース。以上のようにトレードオフの関係が見られる事象は、誰にとっても最良な答えを1つに決めることができないため、解決が難しい問題です。
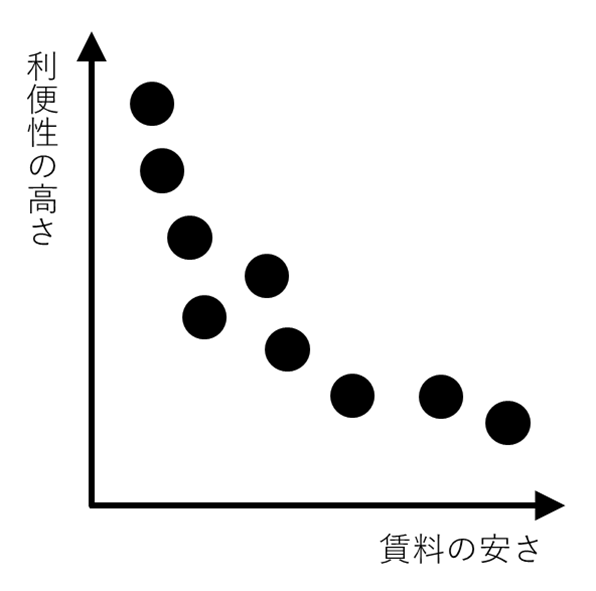
図1. 賃貸マンションの物件を、横軸:賃料の安さ、縦軸:利便性の高さとしてプロットしたグラフ
*1:ソフトウェア業界ではQuality(品質)、Cost(コスト)、Delivery(納期)の頭文字をとってQCDというコンセプトがよく使われます。
材料開発におけるトレードオフ
有用な物質を探す材料開発において、物質を合成する実験条件を決める際にも、トレードオフの関係が出てきます。材料開発では、ある実験条件のもとで物質を合成し、その物性値(e.g. 電気伝導率、強度、延性、安定性)を評価します。物性値が目標とする値に達するまで、実験条件をかえて物質を合成するというプロセスを繰り返します。評価対象とする物性値は分野や目的によって様々で、1種類のときもあれば2種類以上のときもあります。2種類以上の物性値を評価する必要があるとき、すべての物性値が同時に目標とする値を満たすような実験条件を探し出すことはしばしば困難になります。それぞれの物性値が独立に動くのならまだしも、トレードオフの関係にあるとなおさらです。
では評価対象の複数の物性値が互いにトレードオフの関係にある(かもしれない)場合、どのように実験条件を見つければよいでしょうか。まず考えられるのは、物質を合成する際の温度を実験ごとに1℃ずつ変える、原料の配合比を1%ずつ変えるなど、設定可能な実験条件を網羅的に試すというアプローチです。このアプローチはトレードオフの関係があろうがなかろうが使える普遍的な手法ですが、材料開発における実験が1回あたり数時間以上かかることを考慮すると現実的ではありません。あるいは実験者の知識や経験をもとに実験条件を決めるアプローチはどうでしょうか。評価対象の物性値が1種類のときには有効かもしれませんが、2種類、3種類と増えていくに従ってトレードオフの可能性も考慮しながら実験条件を考えることは飛躍的に難しくなっていきます。そこで今回は、コンピュータに最適な実験条件を考えてもらう、多目的最適化のアプローチを紹介します。
トレードオフを解消するための多目的最適化とは
多目的最適化は、トレードオフの関係にある複数の指標を、同時に最大化(最小化)する解を求める計算手法です。多目的最適化を、「多目的」と「最適化」に分けて説明します。
まずは「最適化」です。最適化は、ある条件のもとで得られるなんらかの指標があるとき、その指標を最大化(最小化)する条件を探す手法です。材料開発においては、実験の結果得られる物性値を最適化対象の指標として、その物性値を最大(最小)にする実験条件を探し求めます。最適化の計算には、それまでに得られた実験データ(実験条件と得られた物性値のセット)が必要となります(図2)。材料開発で最適化を用いる場合、最初はランダムな実験条件によって実験せざるをえませんが、実験データを徐々に蓄積しながら数理的なアルゴリズムによって望ましい実験条件を探すアプローチがとられます(*2)。
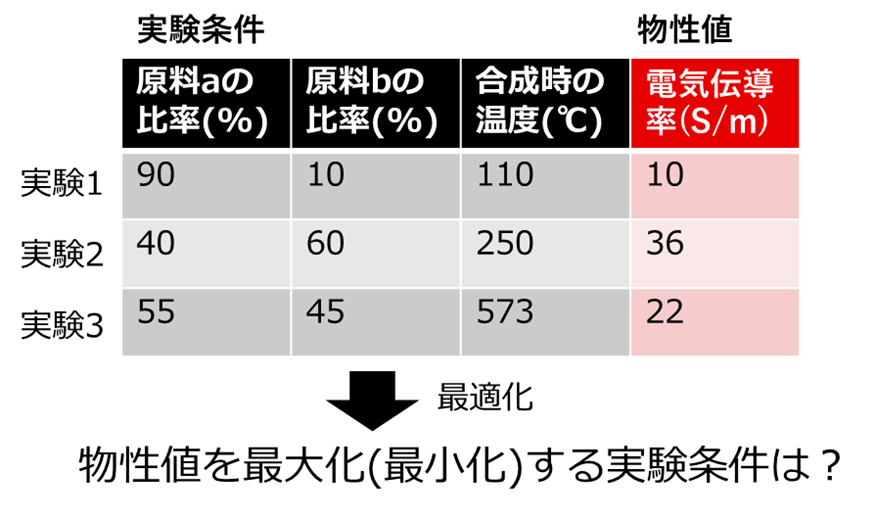
図2. 実験データをもとに最適化を行うイメージ
*2:MKIナレッジ「マテリアルズ・インフォマティクスのABC~ベイズ最適化による賢い実験計画~」を参照。
/knowledge/column150.html
次は「多目的」です。多目的は、最適化対象の指標を同時に複数扱うことを意味しています。指標が複数になると、最適化における解(求めたい実験条件)の探し方が、指標が1つのときと変わります。指標が1つの最適化では、その指標を最大化(最小化)するような1つの解を探す計算を行います。一方、複数の指標を扱う多目的最適化では、指標が互いにトレードオフの関係にあることが多く、そのような場合には最適な解が1つに決まりません。そのため、互いに優劣のつけられない最適解の集まり(パレート解と呼びます)を、効率よく探し出すための計算を行います。
多目的最適化におけるパレート解は、他のすべての解と比べたときに、少なくとも1つの指標で優れている解のことです。具体例を出して解説します。材料開発において、合成した物質を2種類の物性値(物性値1、物性値2)で評価する実験を考えます。横軸:物性値1、縦軸:物性値2としたグラフに、実験結果の物性値を丸としてプロットします。実験条件をかえて3回の実験を行った時点の状態が図3です。赤丸はパレート解、黒丸はパレート解ではない実験結果を示しています。赤丸がパレート解となっているのは、他の丸(赤丸、黒丸)と比べたとき、必ず物性値1もしくは2のどちらかでよりよい値が出ているためです。一方で黒丸は、他の丸(2つの赤丸)と比べたとき、物性値1と2の両方で比較した丸に劣っているため、パレート解ではありません。
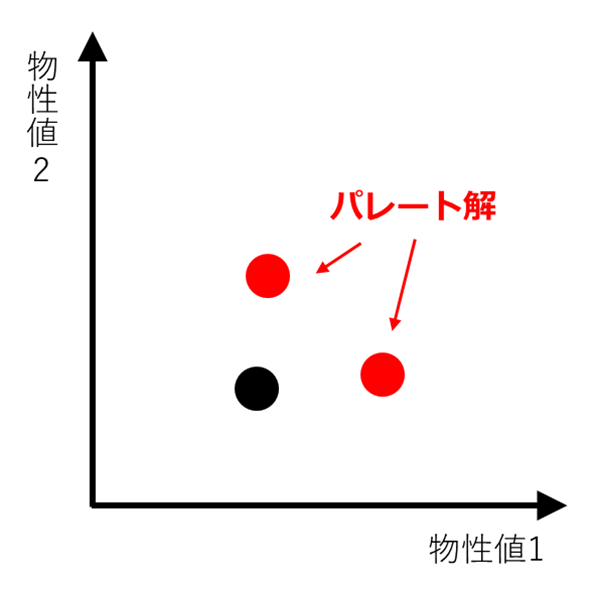
図3. パレート解のプロットイメージ
横軸:物性値1、縦軸:物性値2、それぞれ右と上に行くほど材料として好ましいことを示す。
パレート解となる赤丸を結んで得られる線を、パレートフロントと呼びます(図4)。物性値1と2が互いにトレードオフの関係にあることで、両者ともによい物性値を得る実験条件は存在せず、パレートフロントより右上には丸がありません。パレート解は固定ではなく、最適化の計算と実験を繰り返してよりよい物性値が得られると、以前はパレート解だった赤丸が黒丸にかわることがあります。パレート解を構成する要素にあわせて、パレートフロントの形も変化します。

図4. パレートフロントのイメージ
多目的最適化の計算手順
パレート解を探すための多目的最適化の計算手順について、簡単に説明します。多目的最適化の計算手順として、進化的アルゴリズムやベイズ最適化をベースとした様々な手法が考案されています。今回は、材料開発の分野で使われることが多い、ガウス過程モデルを用いたベイズ最適化の計算手順を紹介します。
ガウス過程モデルを用いたベイズ最適化で多目的最適化を行う流れは、以下のとおりです。
- ガウス過程モデルをつくる
- 獲得関数の最大値を見つける
はじめに、これまでに得られた実験データからガウス過程モデルをつくります。実験条件と得られた物性値の関係を推測し、数式で表現したものがモデルです。ガウス過程モデルをつくることによって、ある実験条件で合成した物質における物性の予測値とその予測の不確かさ(予測がどの程度当たりそうか)を計算できます。多目的最適化では、最適化対象の指標ごとにガウス過程モデルをつくることになります。たとえば、評価対象とする物性値が2種類であれば、ガウス過程モデルも2つ用意します。
次に、パレート解の候補を見つけるため、獲得関数という考え方を導入します。獲得関数は、ガウス過程モデルから得られた予測値とその予測の不確かさをもとに、まだ実験を試していない各実験条件にどの程度見込みがあるかを定量化する基準です。獲得関数が最大になる実験条件は、パレート解の候補として、次に実験を行う提案値となります。獲得関数を導入することで、これまでの実験でそこそこよい物性値が出たときに近い実験条件と、これまで試してこなかった実験条件をバランスよく探索してくれるようになります。多目的最適化においてよく使われる獲得関数として、EHVI (Expected HyperVolume Improvement) があります。EHVIでは既存のパレート解と任意の点(参照点)で囲われた面積(指標が3種類以上のときは体積)を求め、その面積をより大きくするパレート解候補を提案します。面積の計算に、ガウス過程モデルの予測値とその不確かさが用いられているわけです。
ガウス過程モデルを用いたベイズ最適化では、このような流れで多目的最適化のパレート解の候補を提案します。材料開発では、パレート解の候補として提案された実験条件に従って物質を合成し、実際に得られた物性値を評価します。物性値が目標とする値に達していなければ、実験データに実験条件と物性値を追加し、再び実験条件を提案する多目的最適化の計算を繰り返します。
三井情報におけるマテリアルズ・インフォマティクスの取り組み
今回は、評価対象の複数の指標が互いにトレードオフの関係にある状況下で最適化を行うための、多目的最適化のアプローチを紹介しました。三井情報では、東京大学の一杉太郎(ひとすぎ・たろう)教授と中山亮(なかやま・りょう)特任助教との共同研究の一環として、ベイズ最適化で実験条件を提案するWebアプリケーション「MKI-bayesopt(*3)」の開発を進めてきました。これまでのバージョン(V2)では単目的の最適化しか行うことができませんでしたが、2024年9月にリリースした新バージョンV3では多目的最適化に対応しました。その他にも、最適化における制約条件の追加やExcelファイルでのデータアップロードといった機能も導入しています。MKI-bayesopt V3をぜひ触っていただき、ご意見・ご感想をお聞かせください!
*3:「マテリアルズ・インフォマティクス」を参照。/solution/mi.html
関連ページ
おすすめコラム:
マテリアルズ・インフォマティクスのABC~ベイズ最適化による賢い実験計画~
マテリアルズ・インフォマティクスはじめました。
地理空間情報を活用したアプリケーションを実現するアプローチ

阪野
イノベーション推進部 第一技術室
マテリアルズ・インフォマティクスに関する研究開発に従事
コラム本文内に記載されている社名・商品名は、各社の商標または登録商標です。
本文および図表中では商標マークは明記していない場合があります。
当社の公式な発表・見解の発信は、当社ウェブサイト、プレスリリースなどで行っており、当社又は当社社員が本コラムで発信する情報は必ずしも当社の公式発表及び見解を表すものではありません。
また、本コラムのすべての内容は作成日時点でのものであり、予告なく変更される場合があります。





