はじめに
近年では三井情報でもデータサイエンス向けのツールを取り扱ったり、マテリアルズ・インフォマティクスのようなデータサイエンスを中核とする分野に新規参入したり、データサイエンスやAIに関わることが多くなってきました。一技術者である筆者がデータサイエンスをどのように見ているか、一般誌に寄稿した記事を出版社の好意により以下転載します。
-------月刊 Interface(CQ出版) 2022年7月号 pp.22-28 「IT技術者の視点から見たデータサイエンスの世界」 を一部改変し転載-------
データサイエンティストが「21世紀でもっともセクシーな職業」であると言われてはや10年が経ちました(*1)。その後深層学習を中心としたAIブームと相まって、データサイエンスは社会の中で確実に浸透してきたと感じています。
しかしデータサイエンスとは一体何者かと問われるといささか心もとないのも事実です。百花繚乱の様相を呈している技術的な広がりを考えればその理解は100人100様あって然るべきですが、本稿では一介のIT技術者の視点からデータサイエンスの世界を概観してみます。
(*1) 参考:“Data Scientist: The Sexiest Job of the 21st Century” Thomas H. Davenport著、Harvard Business Review 2012年10月号
科学としてのデータサイエンス
データ「サイエンス」というからには、データサイエンスも科学のお仲間になります。では科学とはなんでしょうか。
一般的には図1のような仮説検証のプロセスだとされています。現象になにか法則性がありそうだと気づくところから始まって、仮説とその検証を繰り返しながらその法則性を明らかにしていく試みです。そこで自然現象が起きる物理世界と私の思考を繋ぐのがまさにデータです。
現象学の言葉を借りれば、わたしたちは事象そのものを認識することができませんから(*2)、データを通して世界を見る(見たつもりになる)ことになります。科学において世界を知るにはデータだけが頼りなのです。
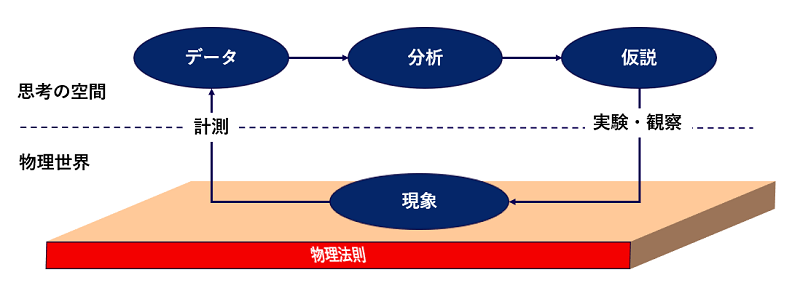
図1
(*2):現象学は哲学的方法論の一種。「事象そのものへ」(Zu den Sachen selbst!)というスローガンを掲げて認識することの本質に迫ろうとした現象学を代表する哲学者フッサールは、事象そのものを認識するためには判断を一旦停止すべし(エポケー)という驚愕の方法を提唱しました。
天文学者のケプラーは世界初の本格的データサイエンティストだった
データから現象を解き明かす「逆問題」
その事情は自然現象を原理原則から紐解く科学の王道、物理学においても同様です。私たちが物理学を勉強するときにはニュートンの運動方程式が与えられた上で振り子の運動を計算するわけですが、ニュートンは現象(≒データ)からスタートして彼の名を冠した微分方程式を導いたのでした(*3) 。運動方程式のような法則が与えられた上で現象を説明することを「順問題」、現象からその法則を推定することを「逆問題」と呼びますが、物理学を理論的に支えているのは(学校での勉強とは違って)逆問題の成果であると言えます。
(*3):『自然哲学の数学的諸原理』(1687年)によって運動方程式や万有引力を含む一連の理論体系が発表されました。
神学的・哲学的だったかつての自然科学
しかし、物理学の黎明期は計算機がまだなかったので扱えるデータ量に限界がありました。神学的要請から提案された仮説を哲学的に議論することが物理学や天文学の主な関心事で、データは主張を補強する程度の従属物だったのです。
そのような状況の中で、ケプラー(図 2)は彼の師であるティコ・ブラーエが残した膨大な惑星の観測データを使って惑星の軌道が楕円軌道であると結論づけたのでした。当時は天動説と「コペルニクス的転回」で有名なコペルニクスの地動説の間で決着がついていませんでしたが、いずれにしても円軌道を前提とした仮説でした。全知全能の神が創造した世界ですから、完璧な対称性のある円こそが神の完全性を象徴するのにふさわしいというわけです。

図2:世界発のデータサイエンティストとされるドイツの天文学者ヨハネス・ケプラー(1571~1630年)
惑星の軌道が円軌道であるという仮説を、データによって楕円軌道に修正した。
神学的・哲学的議論によって成り立っていた事前哲学の世界から、データに基づく現実的な自然科学への道を拓いた。
データを使って現代的な科学の扉を開く
しかしケプラーはブラーエのデータを詳細に検討した結果、円よりも楕円の方が理論的に整合することに気づき、仮説をデータによって修正しました。データを使って仮説を修正するのはまさに現代のデータサイエンティストの精神と同じですね。神学的・哲学的議論によって成り立っていた自然科学の世界にあって、データに基づく現代的な科学への扉を開いたのです。もっともケプラーにしても発想のベース自体は前近代的なもので、「もっとも完全な建設者である神にとって、もっとも見事な作品を創り上げるのは、まったく必然的なこと」と述べています(*4)。
(*4) 参考:『宇宙の神秘』ヨハネス・ケプラー著 大槻真一郎・岸本良彦訳 工作舎(1982年)
モデル(=仮説)の表現力
データに合うようにパラメータを調整する
ここからは仮説のことをデータサイエンスの流儀に従って「モデル」と呼ぶことにしましょう。すると、線形回帰や深層学習といった現代のデータサイエンスで用いる道具はすべからくモデルの鋳型と言うことができます。データを x と表すと、モデル f は一般的に以下のように書けます。
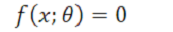
θ(シータ)はパラメータで、モデルの鋳型から特定のモデルを決めるための自由度を与えます。パラメータを調整することでデータを方程式に従わせることが最終的な目標です(*5)。ケプラーが円軌道というパラメータ θc を楕円軌道というパラメータ θe に変更したように、上記の方程式がよりよく成り立つようパラメータを選択するのがデータサイエンティストの(あるいは機械学習器の)仕事になるわけです。
(*5):特に機械学習の文脈では関数近似という言い方をすることがあります。
パラメータ数が多いほど表現力が高くなる
ここで問題になるのが、θ で表現できないものは調整のしようがない、という事態です。図3を見てください(説明の都合上データを x と y の2つに分けています)。どうみても線形回帰ではうまくフィッティングできそうにありません。しかし2次多項式であればそこそこ合いそうです。2次多項式は1次多項式(直線)を包含するので、より表現力が高いことになります。この例から類推できるのは、表現力の高いモデルであればデータが複雑な形状をしていても対応できるということです。ケプラーも円運動に固執せずに楕円軌道も頭の片隅に置いていたために、新しい法則の発見につながったと言えます。線形回帰はパラメータが2つ、2次回帰はパラメータが3つですが、一般にパラメータ数が多くなるほど表現力が高くなります。最近の深層学習モデルでは1,000億を超えるような気の遠くなるようなパラメータ数を持つものも現れています(*6)
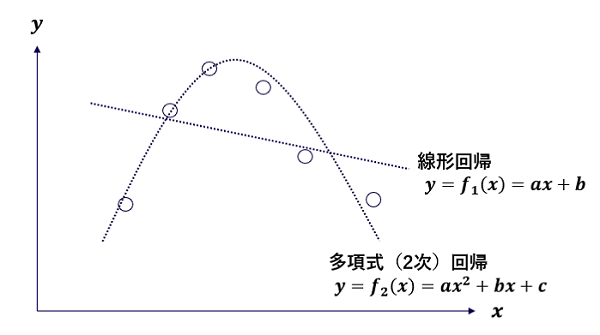
図3 データとそれを表現するモデル(=仮説)
(*6):圧倒的な文章生成能力で世間を驚嘆させたGPT-3はパラメータ数が1,750億でしたが、その後継であるGPT-4は100兆に達するのではないかとも言われています。
統計モデリングvs.機械学習
ここでモデリング(モデルにデータを焚べてフィットさせる行為)には以下の2つの動機があることに触れておきましょう。
①現象を理解したい→現象の表現形態であるところのデータの構造を理解したい・・・統計モデリング
②観測されていないデータがどのような値になるか予測したい・・・機械学習
この2つはある意味で「気分の問題」であり、形式的にはなんら変わりません。線形回帰は統計モデリングであるとも言えるし機械学習であるとも言えるのです。しかし気分の問題で片付けては身もふたもないので、その気分をn次多項式回帰の式で表現してみましょう。
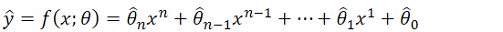
ここで記号「^」は「ハット」と読み、モデルにおける推定値を表します。真の値と一致すれば完全なモデルと言えます。
統計モデリング…現象の理解を追求する
統計モデリングではパラメータの推定値![]() をパラメータの真値 θi にどれだけ近づけることができるかに腐心します。データがおおよそどのような構造になっているかを知ることで、背景にある現象のメカニズムを明らかにしようという動機づけです。その点ではケプラーと一致し、科学的態度と言ってもいいでしょう。統計モデリングでは「現象を適切に表すモデル」を用いることが最も重要であり、結婚相手を探すような慎重さでモデルを選ぶことになります。
をパラメータの真値 θi にどれだけ近づけることができるかに腐心します。データがおおよそどのような構造になっているかを知ることで、背景にある現象のメカニズムを明らかにしようという動機づけです。その点ではケプラーと一致し、科学的態度と言ってもいいでしょう。統計モデリングでは「現象を適切に表すモデル」を用いることが最も重要であり、結婚相手を探すような慎重さでモデルを選ぶことになります。
機械学習…表現力の高さで予測能力を追求する
一方で機械学習ではパラメータ![]() が真の値かどうかなどということに気を揉みません。機械学習においてはデータの一つ y に特別な位置付けが与えられ、これを「目的変数」と呼びます(*7)。目的というくらいですから y を推定することが絶対的な目標になります。従ってパラメータ
が真の値かどうかなどということに気を揉みません。機械学習においてはデータの一つ y に特別な位置付けが与えられ、これを「目的変数」と呼びます(*7)。目的というくらいですから y を推定することが絶対的な目標になります。従ってパラメータ![]() の精度などには目もくれず、あくまで予測対象である ŷ の精度にしか興味がないのです。そうなるとモデル自体にはなんの執着もなく、ファストファッションのようになんの後腐れもなく表現力の高いモデルに乗り換えていくことになります。その極北にあるのが深層学習だといえるでしょう。
の精度などには目もくれず、あくまで予測対象である ŷ の精度にしか興味がないのです。そうなるとモデル自体にはなんの執着もなく、ファストファッションのようになんの後腐れもなく表現力の高いモデルに乗り換えていくことになります。その極北にあるのが深層学習だといえるでしょう。
(*7):機械学習には教師あり機械学習、教師なし機械学習、強化学習などいくつか典型的なセッティングがありますが、ここでは教師あり機械学習に話を限定します。
表現力が高い=予測能力が高い?
パラメータ数が多ければ良いわけじゃない
表現力が高ければ(≒パラメータ数が多ければ)予測能力が高いと言えるのでしょうか。実はそうではありません。図4(a)のようなデータがあったとしましょう。おおよそ3次関数でフィットできそうに見えます(*8)。実際に3次多項式と9次多項式でフィットさせた結果を図4(b)に示します。3次多項式は予想通りの概形をしていますが、9次多項式はデータに極めてよくフィットしているものの(*9)、グラフのスケールが大きく変わってしまうほどトレンドを外れた部分がみられます。これはモデルがデータに適合しすぎた「過学習」と呼ばれる状態です。過学習が起きると既知のデータにフィットしすぎることによって、未知のデータをむしろ外しやすくなります。予測性能が低下するのです。
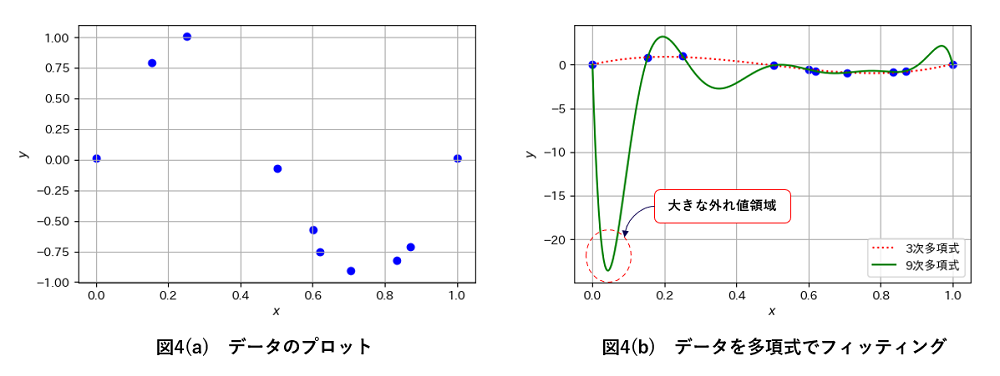
(*8):正弦関数に若干のノイズを乗せて10点生成させました。
(*9):9次多項式はパラメータが10個あるので、10点あるデータを厳密に満たすような解が存在します。
モデルの予測能力を評価するスコア「AIC」
予測能力が表現力の単調増加関数になっていないとすると、何か適切な評価方法がないものでしょうか?あります!統計学者の赤池弘次氏が開発した「AIC」と呼ばれるスコアです。An Information Criterionの略で(*10)、以下のような式で表されます。モデルとデータによってAICが決まり、AIC小さいほど予測能力が高いモデルということになります(必ずそうなることは保証されません)。
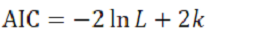
第1項の L は最大尤度と呼ばれる量で、モデルがデータにフィットすればするほど大きくなります。従って、モデルがデータにフィットするとAICが小さくなる→予測能力が高くなります。自然ですね。一方で第2項の k はパラメータ数ですから、パラメータ数が大きくなるとAICが大きくなる→予測能力が低くなることになります。パラメータ数の増加は表現力の向上を通して予測能力向上に寄与しますが、同時に過学習による予測能力の低下も引き起こすという意味です。つまり、パラメータ数が小さすぎても大きすぎてもいけないのです。AICを使うとパラメータ数が予測能力の観点で適正なサイズかどうか判断することができますから(図5)、3次多項式がいいのか4次多項式がいいのか、モデルの選択に用いられます。
AICは情報理論を使ってモデル間の距離を評価する手法の先駆けとなったもので、統計モデル、機械学習の理論解析に大きな影響を与えました。Google検索のロゴが著名人の記念日にあわせて変わることがありますが、2017年11月5日に赤池先生の生誕90周年を記念したデザインが採用されたのは、機械学習研究の一大拠点であるGoogleからの敬意を表しているといえるでしょう。
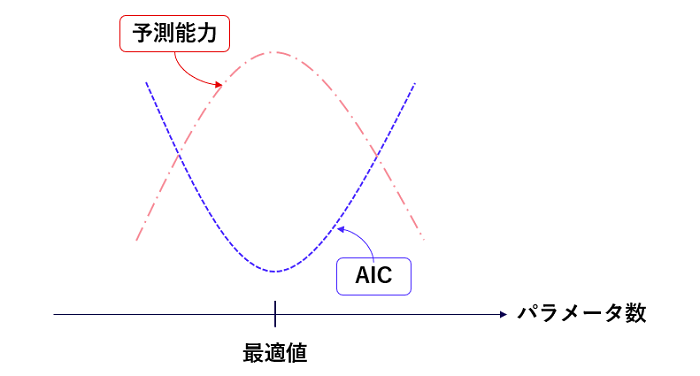
図5
(*10):情報理論を使ってモデル間の距離を評価する手法の先駆けです。AIC以後様々な情報量基準(Information Criterion)が提案されたため、それらと区別するためかAkaike Information Criterionと呼ばれるようになりました。ちなみにAICを一般化して適用範囲を広げたWAICという情報量基準を渡辺澄夫・東京工業大学教授が2009年に発表しましたが、論文ではWidely Applicable Information Criterionと表記されたにも関わらず、業界ではWatanabe-Akaike Information Criterionと呼ばれることが多いようです。渡辺先生がそこまで見越して命名したものかどうか、筆者は知りません。
莫大なパラメータをもつ深層学習はなぜ予測性能が高いのか?
パラメータ数が大きすぎると過学習を起こして予測性能が低下というのであれば、莫大なパラメータ数をもつ深層学習が驚異的な予測性能を示すのはなぜでしょうか。まず前提として、表現力の小さいモデルではとても太刀打ちできないような複雑な構造のデータに対して深層学習が適用されるということがあります。Kaggleのようなデータ分析コンペで出される比較的小規模なデータでは、決定木系のGBDT(Gradient Boosting Decision Tree)が人気です。データの構造よって得意不得意があるのです。小さなデータに対して深層学習を適用しても満足な予測性能は出ないでしょう。
大規模かつ複雑なデータに対しては深層学習の出番ですが、それに見合わないほどパラメータ数を大きくしても単調に予測性能が向上していく傾向が見られます。過学習に陥りにくいのです。なぜそのような性質があるのか理論的な決着はついておらず、学習理論研究界隈のホットトピックになっています(*11)。
(*11):詳細は、この分野の代表的な研究者である今泉允聡・東京大学准教授の一般向け著作『深層学習の原理に迫る: 数学の挑戦』(岩波書店)や論文『深層学習の原理解析:汎化誤差の側面から』(日本統計学会誌第50巻 第2号 pp.257-283、オープンアクセス)などを参照してください。
すべてのモデルは間違っている?
予測能力を追求する機械学習の立場と現象の理解を目指す統計モデリングの立場の対比に話を戻しましょう。そもそもモデル自体が完全に現実と一致するのであればそのような立場の差は生じないはずです。完全な予測能力と完全な現象の理解が同時に得られることになります。
しかし一見シンプルに見えても現実は複雑なものです。完全に一致することは100%ないと言っていいでしょう。そのことをイギリスの統計学者ボックス博士(*12)は次のような気の利いた警句として表現しています。
“All models are wrong, but some are useful.”
間違っているのは仕方ないとしてどこに有用性を求めるか?その観点において現象の理解と予測性能という代表的な2つの流儀があるのだろうと筆者は理解しています。
(*12):機械学習の前処理として使われる変数変換「Box-Cox変換」に名を残しているのをはじめ、品質管理や実験計画といった実践的統計処理分野に数多くの業績があります。
深層学習は預言者か?
機械学習だからといって予測性能だけに興味があるという状況は、とりわけ深層学習において変わりつつあります。
深層学習の圧倒的な表現力を頼りに現象を写し取らせ、学習済み深層学習モデルの中身をさらに解析することで現象に対する理解を深めようという研究が物理学を中心に盛んになってきました(*13)。図6のようなスキームで、深層学習の膨大なパラメータから知識を得るという手法です。
物言わぬ自然現象の言葉を深層学習モデルを通して聞くということですから、深層学習は機械学習の一手法であることを超えて、もはや神の預言者になりつつあるのではないか、とさえ思えてきます。
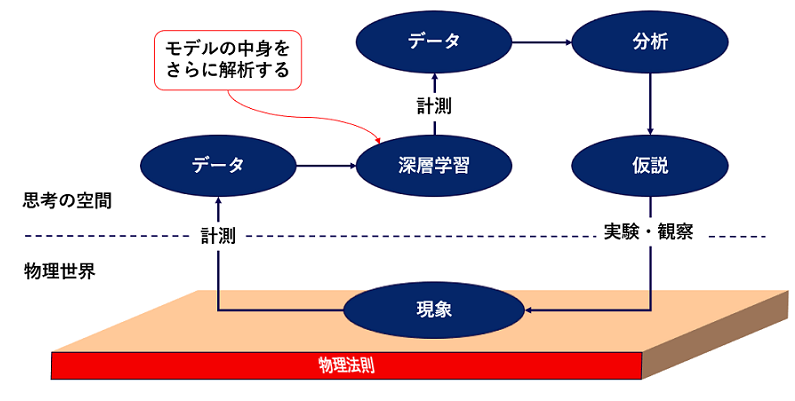
図6 学習済み深層学習のモデルの中身を更に解説するスキーム
(*13):『物理学者、機械学習を使う』(橋本幸士他著、朝倉書店)の中で様々な事例が紹介されています。
データサイエンスのこれから・・・予測から意思決定へ、さらに交渉・協調へ
出口戦略は意思決定にあり
ここまで現象の理解と予測の両面でモデリングについて見てきましたが、ここで予測の使い途について少し考えてみましょう。
意思決定の科学「オペレーションズ・リサーチ(OR)」
予測はそれ自体に価値があるものではありません。予測の先に予測の利用が必ず付帯します。将来値上がりしそうな暗号資産があれば「買う」、今日雨が降りそうであれば「傘を持って外出する」のように、いわゆる意思決定が伴うのです。意思決定の科学はデータサイエンスなどというコンセプトが出現するはるかに前から存在し、「オペレーションズ・リサーチ(OR)」として20世紀はじめ頃から研究されています。
例えば株式取引など金融商品の売買においてはポートフォリオという言葉をよく耳にしますが、典型的なORの技術を利用しています。資産運用の目的は当然資産を増やすことですが、ハイリターンであるほどハイリスクであるという、いわゆるトレードオフが存在します。そこで、①安定している商品(=予測値の分散が小さい)、②値動きが激しい商品(=予測値の分散が大きい)、③お互い同じような値動きをする商品ペア、④お互い逆の値動きをする商品ペア、をうまく組み合わせることで個人にあったリスクとリターンのバランスを調整します。これがポートフォリオです。
一般に意思決定になんらかのトレードオフが存在する場合、いわゆる最適化問題として定式化されます。折りたたみ傘を持っていきたいがそのためにはカバンから持ち物を減らさなければならない、ケーキを食べたいがそのためには食事から炭水化物を減らさなければならない、などです。そこに個人の選好を表す効用関数Uを導入すると、ORがその歴史の中で営々と培ってきた最適化アルゴリズムによって、意思決定を自動的に選択することができるというわけです。
意思決定の最適化プロセス
ここで予測には必ず意思決定が付帯していたことを思い出すと、意思決定には予測が含まれることがあります。つまり最適化のプロセス全体は図 7のような格好をしています。最適化の材料となるのは折りたたみ傘の重さ、ケーキのカロリーといった確固たる事実もあれば、1年後の株価といった予測値もあるかもしれません。せっかく予測のためのモデリングをするのであれば、その先の意思決定・最適化問題まで視野を広げることでより直接的な価値を生み出すことができるというわけです。
ビジネスの世界では事業価値が全てですから、データサイエンスの主戦場は予測単体から最適化も包含する方向に徐々にシフトしていくものと筆者は予想しています。最適化はそれ自体非常に難しい分野ですが(*14)、統計モデリングや機械学習を使いこなす技術と最適化の技術を併せ持てばまさに鬼に金棒でしょう。
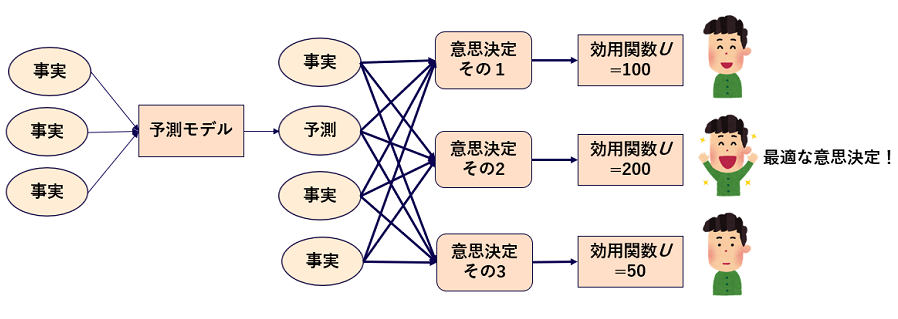
図7 意思決定の最適化プロセスの全体像
(*14):最適値を求めるのが難しい複雑な問題に対して「双対問題」とよばれる数学的に反転させたような問題を組み合わせて最適値(の近傍)を探索したり、計算量爆発や解が一つも出ない状況に対して問題の”緩和”を施したり、様々なテクニックを駆使する必要があります。
相関と因果を混同してはいけない
チョコレートの消費量とノーベル賞受賞者数
意思決定で一つ注意しなければならないのは、相関関係を以て因果関係と見なしてはいけないということです。
これは多項式回帰のように x と y の関係をモデリングした後、x を操作する(意思決定する)ことで y の値を変化させるような最適化タスクで現れます。この類の議論をする際によく引き合いに出される有名な研究論文がありますので(*15)。主結果を表すグラフ(図8)を見てみましょう。
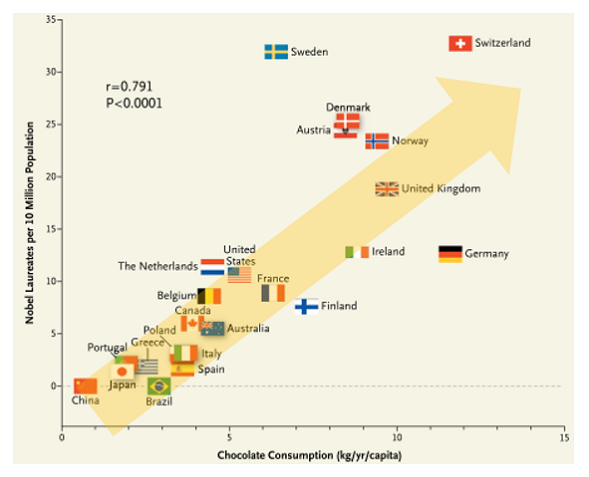
*図8 相関関係をもって因果関係とみなしてはいけない例
横軸が各国の人口あたりチョコレート消費量、縦軸が人口あたりノーベル賞受賞者数になっています。一見して右肩上がりのトレンドがありそうです。「なるほど、チョコを食べればノーベル賞がもらえるのだな。じゃあ全国民に無料でチョコレートを配ればノーベル賞受賞者が増えるのでは... 」これは直感的にかなりあやしい結論です(*16)。一体どこがおかしいのでしょうか。
*図8 引用元:F. H. Messerli;“Chocolate Consumption,Cognitive Function,and Nobel Laureates”,The New England Journal of Medicine,Vol.367,No.16,pp.1562-1564,Oct. 18,2012.
(*15):Messerli,F.H.,(2012). “Chocolate Consumption, Cognitive Function, and Nobel Laureates” N Engl J Med, 367, pp.1562-156 Box4.
(*16):NewEngland Journal of Medicineという医学系の超一流誌に荒唐無稽とも思える主張の論文が掲載されたため論争となりましたが、著者が本気でそう考えたのかどうかは分かりません。
共通の原因があるため因果関係ではない相関関係が見える
断定はできませんが、真の因果関係は図9のような状況になっているものと推測されます。共通の原因があるために、因果関係ではない相関関係が見えているのです。機械学習が同定するのはあくまで相関関係ですから、それを因果関係であると早急に結論づけてはいけません。この例のような間違いを犯す可能性があります。
ではどうすればいいのでしょうか。基本的には実験する以外に手がありません。図1の描像で言えば、物理世界に実験という形で介入することを意味します。観察しただけでは因果関係がわからないのです。
因果関係を同定するための実験では、注目すべき変数(例えばチョコレート消費量とノーベル賞受賞者数)以外の変数を揃えた上で、一方の変数を変化させたときにもう一方も反応するかどうかを評価します。このような実験の組み方は「実験計画」という学問分野として確立していて、ワクチンや治療薬の効果検証(業界では臨床試験と呼びます)にも利用されています。
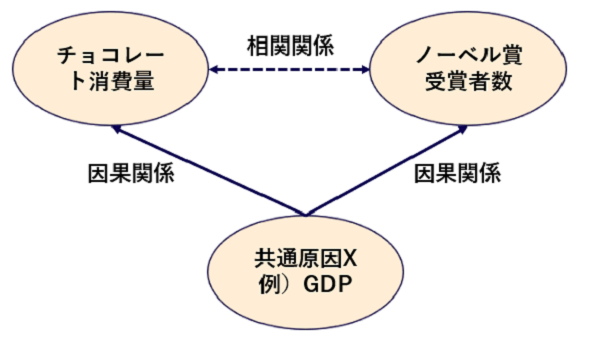
図9
進化する因果推論
チョコレートとノーベル賞のような因果関係を評価する場合に、「注目すべき変数以外の変数を揃える」国や地域を複数準備することは現実的に不可能です。タバコと肺がんの関係を調べるような場合でも、タバコを吸う人と吸わない人を人為的に割り振ることは倫理上できません。このように管理された実験が事実上不可能な状況において、観察データからあたかも実験したかのような仮想的なセッティングを構築する手法が近年開発され、実際社会問題等に適用されるようになってきました。2021年のノーベル経済学賞受賞対象の「自然実験」がそれに該当します。
因果関係を統計理論によって推定する学問分野を「統計的因果推論」と呼びますが、医療や社会科学において限定的に使われていたこの技術が、自然実験のような進化に伴ってマーケティングなどビジネスの現場で使われることも多くなっている印象を受けます。データサイエンスがその守備範囲を広げている一例と言えるでしょう。
多数のエージェントが交渉・協調する世界へ
ここまで見てきた意思決定は、個人や一企業など単独のエージェントがその力の及ぶ範囲で最適な行動を選択するという前提に立ったものでした。しかしそれでうまくいくとは限りません。
例えば車の交通流最適化というタスクを考えてみましょう。多数のエージェントが自分自身の最適行動を取った結果あるルートに集中してしまえば、もはやそのルートは誰にとっても最適ではありません。その場合には多数のエージェントを指揮するような、例えばGoogleマップのナビゲーションのような支配的最適化エージェントをあらためて置けば全体最適が実現します。
しかしそれではいわゆる単一障害点になってしまいますし、その支配関係を悪用される可能性もありますから、とりわけ社会システムにおいては望ましい姿と言えないでしょう。そこで、エージェント同士が交渉・協調しながら結果的に全体最適に達する仕組みが必要なのでないかと考えています。まだそのような実践をあまり耳にしませんが、予測と(個別)最適化をベースにしたアルゴリズム設計になることは疑いなく、データサイエンスの将来的課題の一つになっていくのではないでしょうか。
筆者の見ている範囲では、データサイエンスは図 10のような発展史をたどっています。みなさんも是非、手を動かしながらデータサイエンスの諸相を楽しんでください。
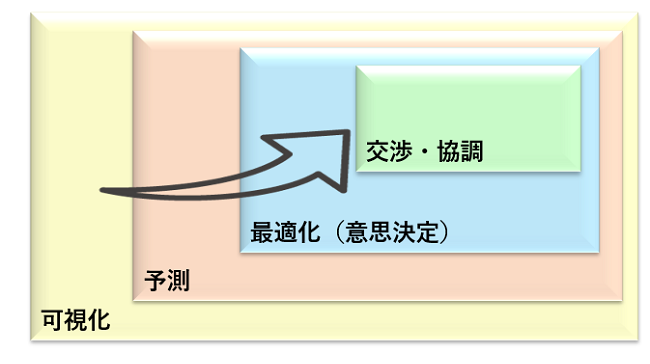
図10 筆者の視点から見たデータ・サイエンスの発展史
関連ページ
おすすめコラム:
マテリアルズ・インフォマティクスはじめました。
未来を予測すること -需要予測を例として-
関連ソリューション:
マテリアルズ・インフォマティクス
バイオインフォマティクス

中島
技術推進部
現在、シミュレーション技術の調査研究、マテリアルズ・インフォマティクス向けアプリケーションの開発、社内教育活動に従事。
コラム本文内に記載されている社名・商品名は、各社の商標または登録商標です。
本文および図表中では商標マークは明記していない場合があります。
当社の公式な発表・見解の発信は、当社ウェブサイト、プレスリリースなどで行っており、当社又は当社社員が本コラムで発信する情報は必ずしも当社の公式発表及び見解を表すものではありません。
また、本コラムのすべての内容は作成日時点でのものであり、予告なく変更される場合があります。

