三井情報では、数年前からマテリアルズ・インフォマティクス分野に携わるようになりました。中国等に猛追されている日本のお家芸「ものづくり」。その国際競争力維持・向上に少しでも力になりたいと考えたからです。しかしマテリアルズ・インフォマティクスはまだ新しい概念のため具体的な中身をご存知の方は少ないと思いますので、その一端を垣間見ていただくべく、一般誌に寄稿した解説記事を出版社の好意により転載します。
-------月刊Interface(CQ出版) 2022年7月号 pp.66-72 「材料組み合せ最適化マテリアルズ・インフォマティクス」 を一部改変し転載-------
マテリアルズ・インフォマティクス(MI)とは?
素材と情報科学の組み合わせたもの、2011年から
「マテリアルズ・インフォマティクス」とは、見た目の通りマテリアル(物質・素材)とインフォマティクス(情報科学)を組み合わせた造語です。
いつ誰が言い出したのか定かではありませんが、その火付け役となったのは2011年にアメリカでスタートした国家プロジェクト、「Materials Genome Initiative」と言われています。新しい機能性材料の探索~実用化までのリードタイムを情報技術の力で半分にするという超意欲的な試みで、5億ドルの巨費が投じられて各種計算モデルやデータベースが整備されました。「より早く(開発する)」がメインのスローガンでしたが、それと同時に「より高品質(高機能)に」「より低コストで」という要請とも表裏一体ですので、IT業界でよく言われるQCD(Quality, Cost, Delivery)をいっぺんに底上げする試みと捉えていただくとわかりやすいと思います。
材料開発は日本のお家芸、遅れをとるわけにはいかない
その後、先進各国にその流れは広がり、5年ほど前から国の研究機関(物質・材料研究機構や産業技術総合研究所)を中心に日本版のインフラ整備が始まりました(※1)。元々我が国の材料開発産業は長年にわたって世界をリードしてきたので、ここで遅れをとるわけにはいきません。国の重要な研究開発分野に位置付けられました。
(※1)参考:情報統合型物質・材料開発イニシアティブwebサイト(更新終了)
https://www.nims.go.jp/MII-I/
その活用方法は民間に委ねられた
しかし、国はあくまで共通基盤や基礎科学としての知見を造ることがその役割です。最終的にマテリアルズ・インフォマティクスを社会価値に還元していくのは民間自身の力です。そのようなわけで最近は大手メーカーを中心にマテリアルズ・インフォマティクスの活用が進んでおり、ITベンダも参入し始めています。
なお、以降は慣例に倣ってマテリアルズ・インフォマティクスをMIと略します。
データサイエンスの観点から見たMI
JSTによるMIの定義
日本のMI研究を牽引している科学技術振興機構(JST)は、2013年の戦略プロポーザル(※2)の中でMIを次のように定義しています。
「計算機科学(データ科学、計算科学)と物質・材料の物理的・化学的性質に関する多様で膨大なデータとを駆使して、物質・材料科学の諸問題を解明するための科学技術的手法」(下線筆者)
(※2)参考:JST研究開発戦略センター 戦略プロポーザル「データ科学との連携・融合による新世代物質・材料設計研究の促進(マテリアルズ・インフォマティクス)」CRDS-FY2013-SP-01
材料から物性を導出したいがそう単純ではない
企業や大学に多くの専門家がいる
MIにデータ科学、計算科学がどのように適用されているのか、図1を使ってご説明します。緑色の網掛け部分がMIの技術的実体です。
MIのそもそもの目的は、機能性材料の開発にあります。つまり、ある物質 Xm(図1の②)がどのような物性 y(図1の③)を持つかを明らかにすることがその本質です。私たちは物質が従う基本方程式(「支配方程式」と呼ぶならわしがあります)を知っていますから、物質情報が与えられれば、その物性をシミュレーションすることができます。これが「計算科学」の主な実体です。これはMIが提唱される以前から営々と築き上げられてきた技術領域で、大学にも民間企業にも多くの専門家が存在します。
しかし、どんな系でも計算できるわけではありません。様々な物質や環境が絡む複雑な現象は、原理的には計算できても、現実的な時間では計算が終わらない状況が多々あります。MIではとりわけこの問題が顕在化します。
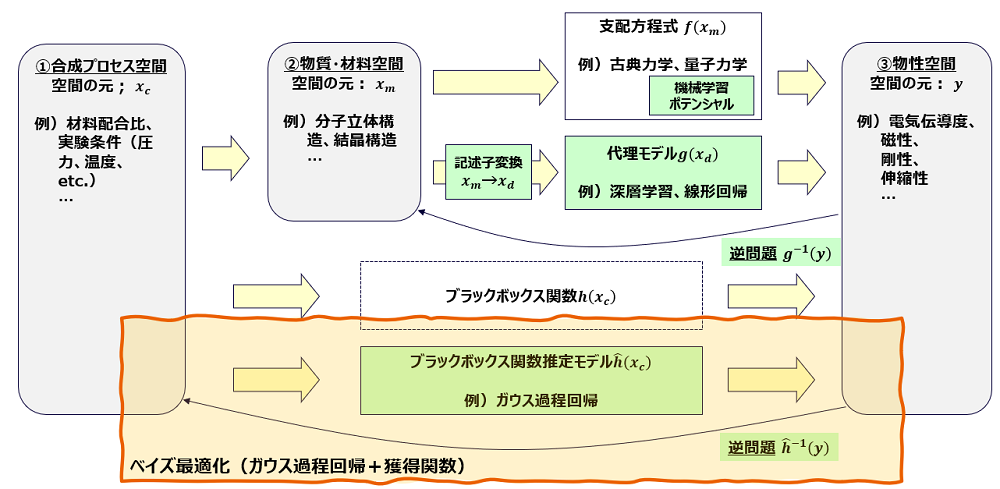
図1:MIの見取り図
材料の組み合わせは無限にある
なぜでしょうか。それはMIが物性 y を固定した上で、y を実現する物質 Xm を探索するという問題設定になっていることに関係しています。Xm はそれこそ星の数ほどあるのですから、可能性のある材料をすべて支配方程式から計算していたのでは富岳のようなスパコンを使っても到底間に合わないのです。このような状況は、原因から結果を求める「順問題」との対比で「逆問題」と呼ばれ、一般的に順問題よりも難しいことが多くなります。
MI登場以前は勘と経験が頼り
コンピュータが使えなければカンピュータということで、MI以前は材料開発者の勘と経験に基づいて実験をすることに頼っていました。
機械学習のアプローチは効率が良い
そこで登場するのが機械学習に代表される「データ科学」の枠組みです。支配方程式はちょっと脇に置いて Xm と y の対応関係のみに着目し、線形回帰や深層学習といった学習器によってその相関関係を表現する方法です。支配方程式を代替するモデルということで「代理モデル」(英語のままサロゲートモデルということもあります)と呼ばれたりもします。支配方程式によって原因から結果を地道に計算する演繹的アプローチと比べて、相関関係を元にパターン化されたモデルによって計算する帰納的アプローチの方が一般的に高効率であるところが最大の特徴です(※3)。逆問題とデータ科学は相性が良いのです。
(※3):その理由の一つは、入力データを単純に加減乗除するような演算過程で済むことによります。支配方程式は微分などの演算子を含んでいるためそう単純にはいきません。
材料をどのように記述してデータに変換するか
コンピュータに食わせる最適な表現
ここで注意すべきは、図1の②を表現するデータは一意ではないということです。ある物質(の状態)を表すものであればなんでもデータになり得ますから、H2Oのような化学式でもいいですし、画像識別のノリで電子顕微鏡写真そのものでもOKです。とにかく物質オブジェクトであるところの Xm を、機械が受け付けられる「記述子」 Xd に変換すればよいのです。機械に入力できればなんでもよいとはいうものの、実用上は物質としての特徴を十分表現しながら機械学習にも乗りやすいというバランス感覚が必要で、化学分野ではSMILES(スマイルズ)という記法がよく用いられます。
例えばグルコース(ブドウ糖)をSMILESで表現すると、図2に示すように、
❝OC[C@@H](O1)[C@@H](O)[C@H](O)[C@@H](O)[C@@H](O)1❞
となります。
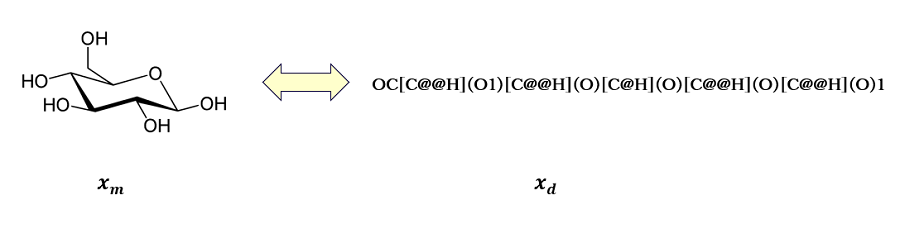
図2:グルコースの表現方法
1つの分子がシーケンシャルな文字列として表現されますので、例えば自然言語処理系の機械学習モデルに比較的容易に適用することができます。しかし、基本的なSMILES文法では一つの分子が一意に表現できないことがあり、一意にするための文法を追加したcanonical SMILESという記法も存在します。物理世界を記号化する難しさの一端が垣間見えているのかもしれません。
ちなみに結晶のような分子の集団構造はSMILESでは表現しきれないわけですが、トポロジーという数学を応用したTDA(※4)(Topological Data Analysis)や、産業技術総合研究所が開発したML-LSA(※5)で記述子化することが試みられています。
図1には②と③の対応関係だけではなく、①(合成プロセス)と③の対応関係にも同じようなモデルの箱と逆問題の矢印が書かれています。
本稿の主眼は実はその部分にあり、合成プロセスを最適化するという観点からMIを体感してみましょう。
(※4)参考:統計数理研究所 プロジェクト紹介「物質科学への応用に向けた位相的統計理論の構築」
https://www.ism.ac.jp/ism_info_j/labo/project/135.html
(※5)参考:産業技術総合研究所 プレスリリース「液晶がナノ構造をつくる際の新現象を発見」
https://www.aist.go.jp/aist_j/press_release/pr2021/pr20210910/pr20210910.html
材料合成の最適化をどのように実現するのか
材料開発の最終章は、実際に材料を作って(合成して)その機能を評価することです。具体的には図1の②と③の対応関係を調べることで物質 Xm の候補をある程度絞り込んだ後、配合比や焼成温度などの実験条件を振りながら最適な条件を見つけることが相当します。ここでは図1の「ベイズ最適化」というMI技術に沿ってその方法をご紹介します。
線形回帰のような単純なモデルでブラックボックス関数の概形を推測するのは至難の業
まず問題となるのが、図1の①と③の関係がブラックボックス関数だということです。私たちは図1の②と③の間にある支配方程式のような知識を持ち合わせておらず、変数 Xc を入力したときにどのような応答 y が返ってくるのか全く不明だという状況を意味しています(※6)。そうすると実験して応答を確かめるより術がありません。全条件を網羅的に調べれば真の関数 h(Xc) を見つけられますが、今の目的は所望の水準の物性 y を発見したいのであって関数を同定することではないのですから、そこまでする必要はありません。できるだけ少ない実験回数で目的となる物性を見つけることを考えます。
(※6):断片的な知識がある場合にそれをモデルに織り込む方法として、ベイズ機械学習やデータ同化といった技術が近年著しく発展しています。
例えば図3のような状況において y の最大値を見つける場合は、
- y が大きくなりそうな Xc = Xc1 を一つ選んで実験をする
- その点での y1 が判明する
- それよりも y の値が大きくなりそうな Xc = Xc2 を選んで実験する
- その点での y2 が判明する
- 以上を繰り返す
として、最終的に y が最大となる Xc を特定するような段取りを踏めばよさそうです。この方法では「今までわかっているよりも y が大きくなりそうな Xc を選ぶ」ために、真の関数 h(Xc) がおおよそどのような形をしているか、それまでの試行結果に基づいて判断することが目標になります。
図3では3点探索した時点で y3 が最大になっていますが、図4のようになんとなく Xc3 より少し右側に y の最大値がありそうな気がしないでしょうか。 Xc と y の関係を表す真の関数 h(Xc) が h1(Xc) のように緩やかな凸関数となっていればまさに予想的中!ですが、h2(Xc) のように細かく振動する関数であれば残念、最小値に近いところをつかまされることになってしまいます。というわけで、線形回帰のような通常のモデルでブラックボックス関数の概形を求めるのはそもそも至難の業なのでは?という気がしてきます。
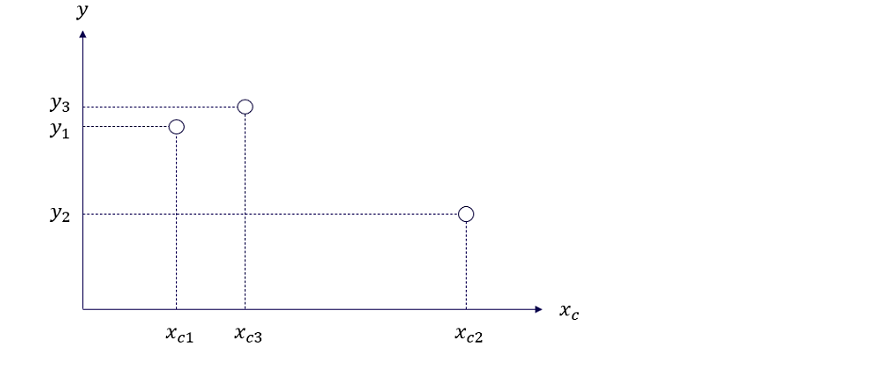
図3
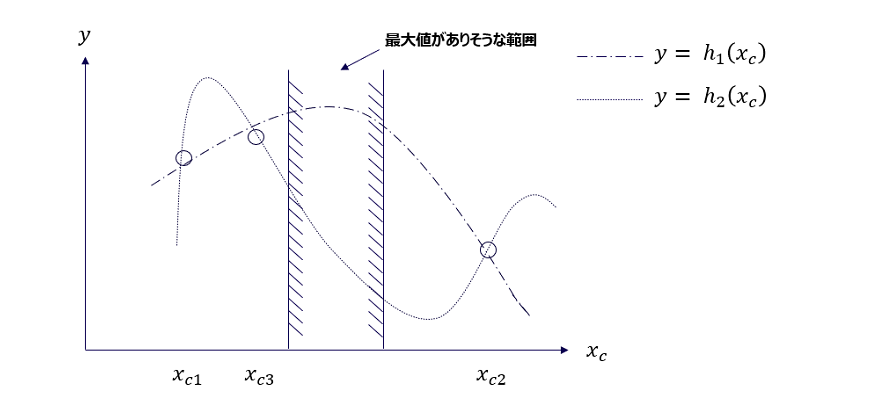
図4
ガウス過程回帰によるブラックボックス関数の推定
そこでガウス過程回帰の登場です。ガウス過程回帰は、モデリングの原点とも言える次の考え方をベースにしています。
「入力 Xc が似ていれば出力 y も似ている」(*)
得られているデータは3点しかありませんが、*の原理をすべての Xc に適用して推定するのです(※7)。しかし「似ている」というあいまいな表現ではアルゴリズムになりません。その定量的関係を与えるのがカーネル関数(※8)というルールで、Xc の各点の間のつながり方を規定します。さらにある制約(※9)を課すと、得られているデータだけを使ってすべての Xc での y の値を一意に決めることができます。
(※7):データのないところの値を推定するためにモデリングをするのであって、ないデータを使って推定するというのは自己矛盾ですが、データのあるところもないところもx_cの各点に関数の素材(基底関数と言います)を用意して、その素材の中から*を満たすように関数を選び出すイメージになります。線形回帰のように関数のパラメタを調整して関数形自体を変える「パラメトリック回帰」に対して、関数の素材の中から組み合わせ方を選ぶこの方式を「ノンパラメトリック回帰」ということがあります。パラメタがないという意味ではなく、少数のパラメタで関数形を決める方針をとらないということです(ガウス過程回帰のパラメタは無限個)。深層学習もノンパラメトリック回帰の一種とみなすことができて、非常に応用範囲の広い考え方です。
(※8):カーネル関数としては動径基底関数(RBF)、Matern3/2など多数の種類があり、いわゆるハイパーパラメタとしてユーザの選択に任されます。どのカーネル関数が最適なのかは h(Xc) がわからないと決まらないという問題先送り的な構造があるのですが、真の関数についての知識がない場合にはガウス分布と同じ関数形をしているRBFがよく使われます。
(※9):計測値(データ)と推定値の誤差に対する「L2ノルム」という制約です。
探索と活用…獲得関数による意思決定(実験条件選択)の最適化
もちろん関数形が一意に決まっただけでは線形回帰と何も変わるところがなく、問題の根本解決にはなっていません。ハズレを引く可能性は大いにあるのです。しかし、ガウス過程回帰には決定的な利点があります。ガウス過程回帰 Xc の各点における y の平均値とその y がどれだけばらつく可能性があるか、ばらつきの幅を示してくれるのです。ばらつきの幅がわかれば、単に y の平均値が大きいところではなく、y のばらつきの大きさも考慮して次の探索点 X4 を決めることができます。この概念を一般に「探索と活用」と表現します (※10)。
(※10):今までよかったところばかりあさる(=活用)のではなくて、未経験な領域も探してみる(=探索)ことで最適な意思決定にするという意味です。これは意思決定全般に当てはまる強力な概念です。
具体的な状況を考えましょう。平均値はあまり大きくなくてもばらつきが大きければ次の実験条件として試してみる価値があります。最大値に近い値を引き当てられるかもしれません。かと言ってやみくもにばらつきが大きいところばかり狙っても平均値が小さければ効率が悪いでしょう。あくまでも平均値とばらつきのバランスを取ることが重要です。そのバランスを取る関数が「獲得関数」です。図5のような状況で機械的に戦略を決定してくれるものになります。
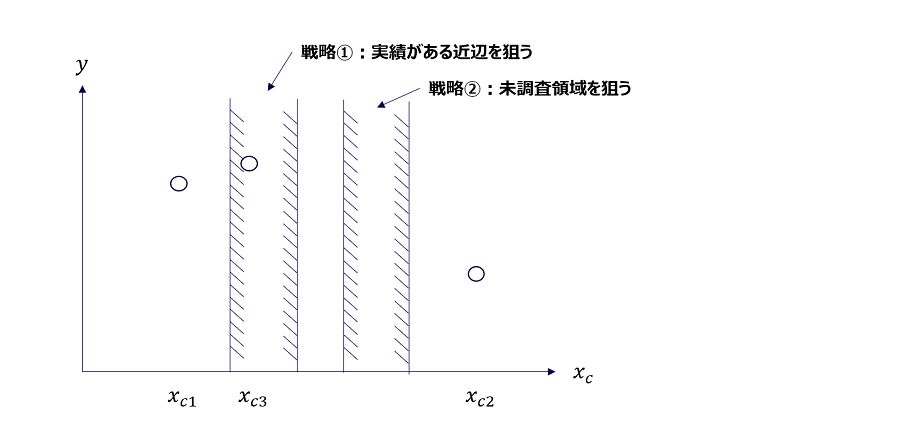
図5
たとえばUCBという基本的な獲得関数は以下のような格好をしています。
UCB (Xc ) = E (Xc ) + κ ∙ σ (Xc )
E は平均、σ はばらつき(分散)を表します。κ がまさに「探索と活用」のバランスを取るパラメタに相当します。ちなみに E も σ もガウス過程回帰から求まる値ですからUCBはその中にガウス過程回帰を含んでいると言えますが、一般に獲得関数は真の関数 h(Xc) を近似する確率的関数 ĥ(Xc) (ここではガウス過程回帰)を引数とする汎関数の形をしています。
最適な実験条件を逐次探索していくというこの問題設定において獲得関数は大きな恩恵をもたらします。探索初期には y のばらつきが大きくなりがちですので全体を大雑把に調べるモード、探索が進むと最大値がありそうな領域がおおよそ絞られてきますのでその近傍を詳細に調べるモード、と適応的に戦略が変化するため、探索効率が非常に高いのです。材料開発に即して言えば実験コストと時間の節約を意味し、まさにMIの目的が達成されることになります。
ガウス過程回帰と獲得関数を組み合わせて実験条件を最適化する方法を「ベイズ最適化」と呼んでいます。ガウス過程回帰のデータを追加しながら確率的関数を更新する部分にベイズ統計(※11)が使われていることに由来します。正確にはガウス過程回帰以外のベイズ統計を使った方法もあり得ますが、ブラックボックス関数を最適化する手段(※12)としては、ガウス過程回帰によるベイズ最適化のほぼ一択というのが現状です。ベイズ最適化や獲得関数といった様々な概念が出てきて混乱しがちですので、それらの関係を図6にまとめます。
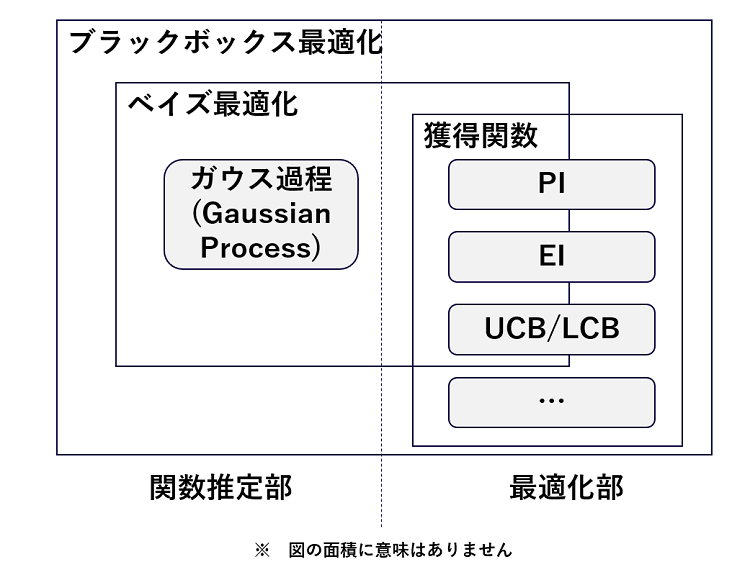
図6
(※11):ベイズ統計に関する教科書は数多く出版されていますが、平易な言葉で基礎原理からベイズ最適化を含む応用例まで豊富に紹介している書籍として「ベイズ推定入門」(大関真之著、オーム社)を挙げておきます。
(※12):ブラックボックス関数の最適化(ブラックボックス最適化と省略します)と同様な概念として、不確実性の下で最適な値を取得するという意味でのuncertainty samplingや、学習データを能動的に選択するという意味でのactive learningがあります。
Pythonでベイズ最適化の挙動を体験する
インストール
ベイズ最適化を実行できるオープンソースのPythonライブラリはいくつかありますが、ここではGPy/GPyOpt(※13)を使うことにします。Python実行環境はGoogle Colabを前提とします。
(※13):英・Sheffield大学の研究グループが開発・メンテナンスをしており、簡単な設定でベイズ最適化を実行できます。またBSD 3-clauseライセンスのため商用利用も可能です(2022年2月現在)。
まずpipでインストールし、関連ライブラリを呼び出しておきましょう(リスト1、リスト2)。

リスト1

リスト2
次に真の関数をリスト3のように定義します(※14)。異なる振動数の三角関数を合成したもので、最小値をとる Xc を求める設定とします。
h(x) = cos(0.5∙2πx)∙sin(0.2∙2πx)

リスト3
(※14):ベイズ最適化の計算エンジンから見ればブラックボックスになっているという問題設定です。
真の関数を描画してみましょう(リスト 4)。Xc=3付近に最小値があることがわかります(図7)。

リスト4
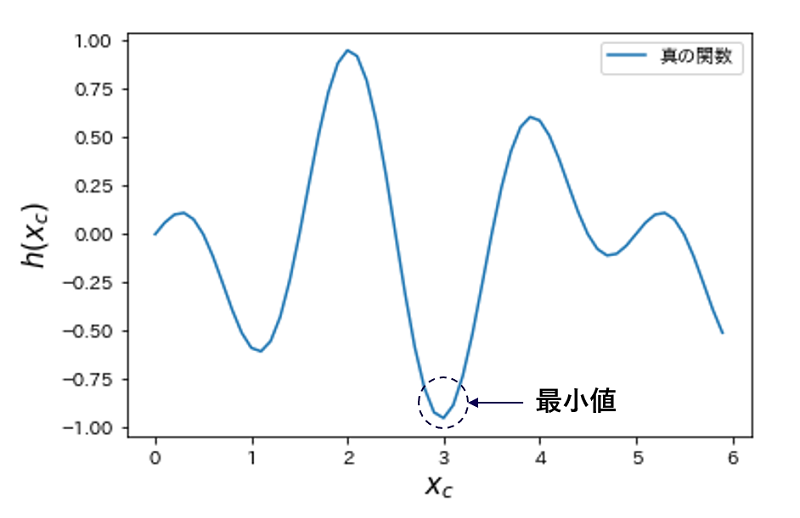
図7
最適化実行
いよいよベイズ最適化の実行です。定義域の両端のみ強制的に探索させてから、獲得関数LCB(加減信頼区間)によって15回探索させてみます(リスト5)。読者の方も再現しやすいように、ベイズ最適化計算だけでなく描画もGPyOptのライブラリを用いています(内部的にはMatplotlibが呼び出されています)。

リスト5
結果の分析
結果を図8~図12に示しました。グラフの下側で横に伸びる赤線が獲得関数の値、垂直に伸びる赤線が次回探索する提案値です。獲得関数を最大にする Xc が、次回探索される Xc に対応しています。
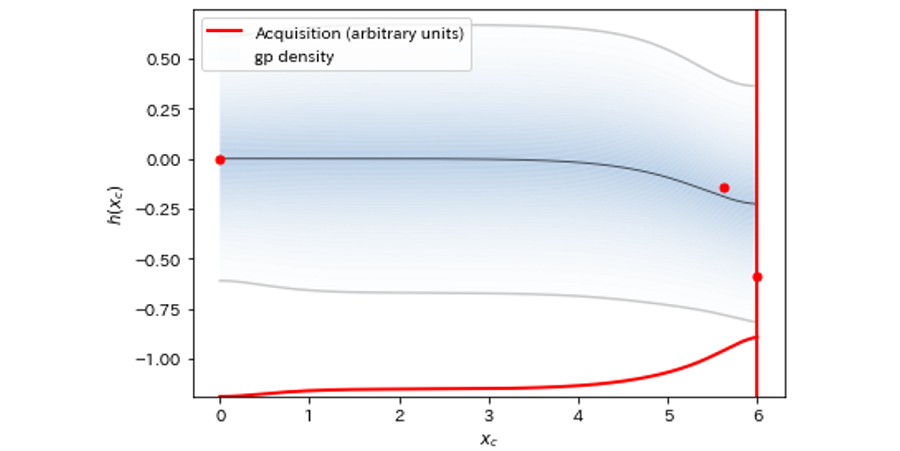
図8:探索回数=3
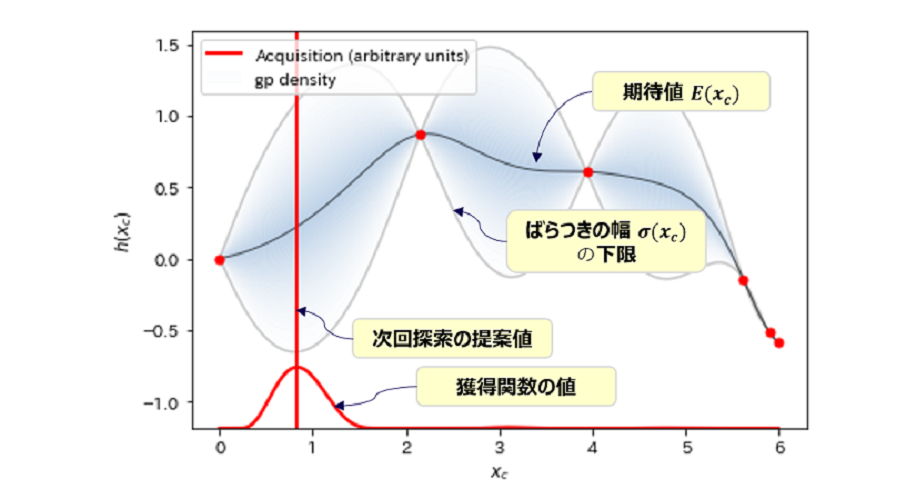
図9:探索回数=6
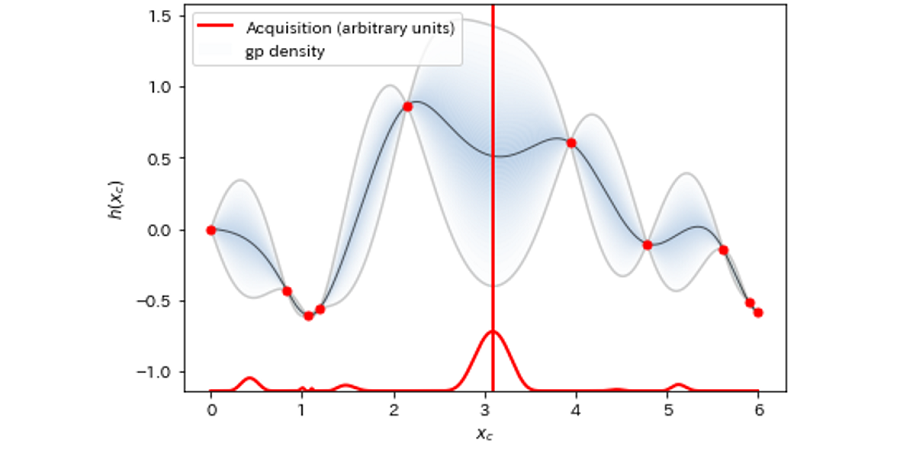
図10:探索回数=10
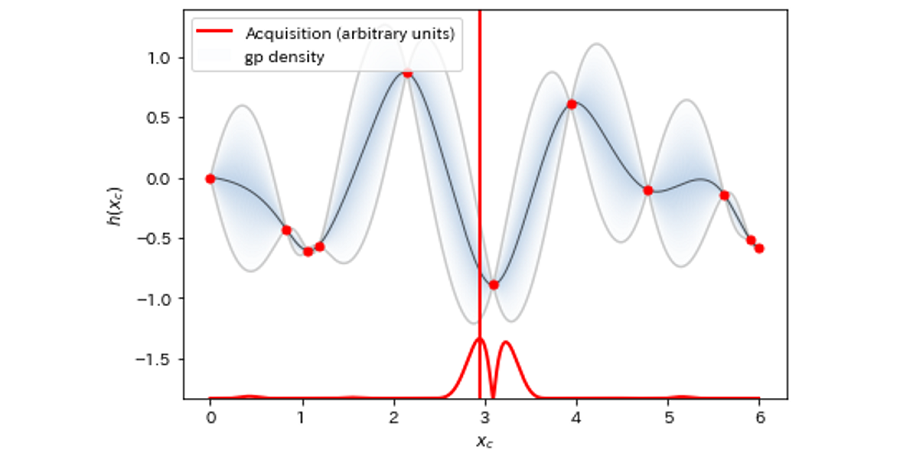
図11:探索回数=11
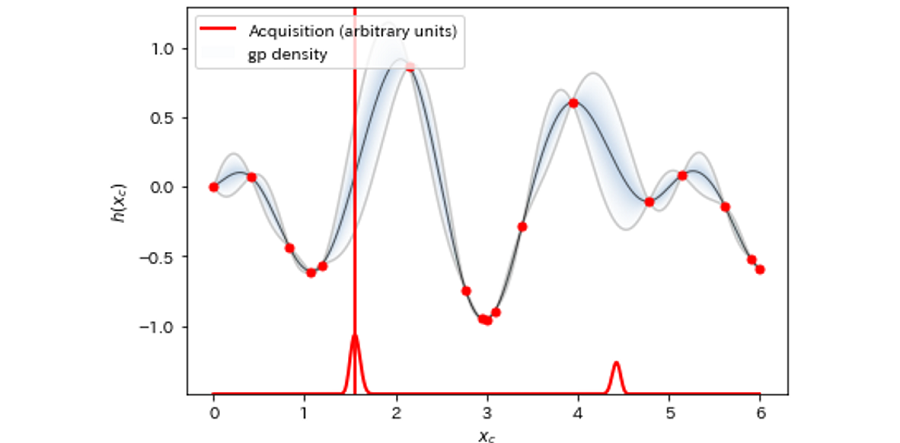
図12:探索回数=17
最初の3回の探索ではまったく関数の体をなしていなかったものが、おおよそ10回程度の探索で真の関数の概形に近づいていることが見て取れます。さらに11回目の探索で重要なイベントが起こります。最小値近傍の”谷”を初めて発見したのです。その後17回まで進めるとかなり真の関数に近づいてきますが、最小値探索という意味ではほぼ11回目で達成していることになります。そのことを示すのが図13です。
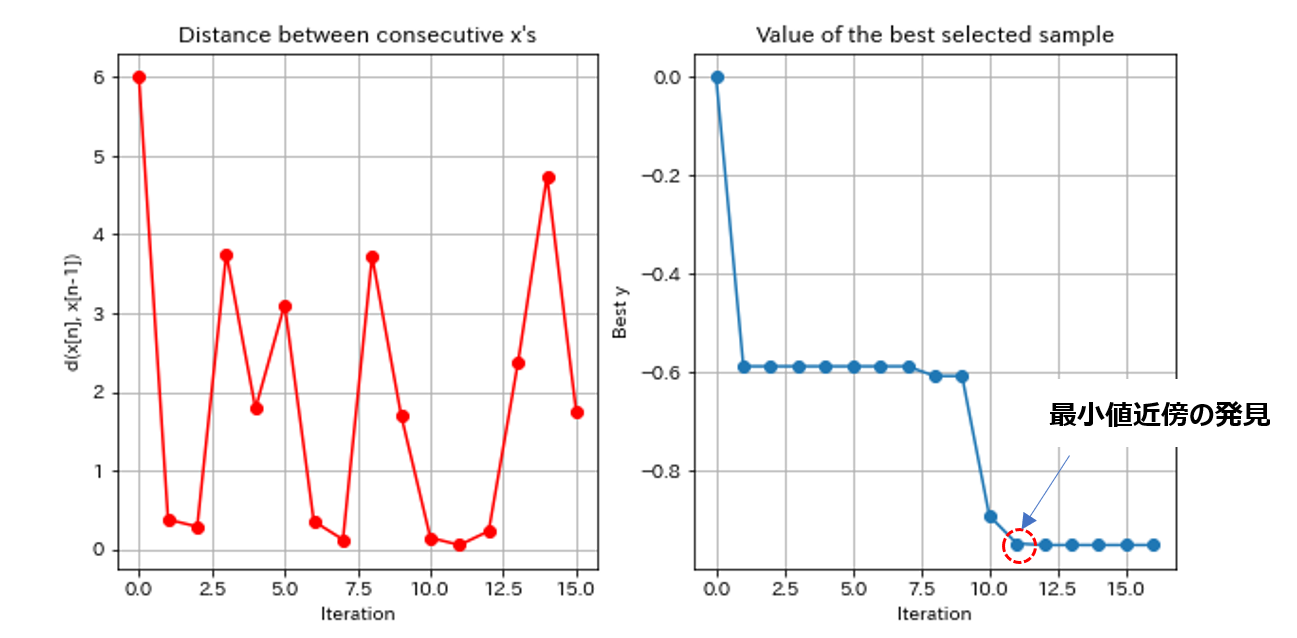
図13:ある探索と次の探索における Xc の距離(左図)、ある探索時点での最小値(右図)
真の関数の形状にもよりますが、ベイズ最適化を用いるとランダムサーチ(探索する Xc をランダムに決定)やグリッドサーチ(探索する Xc の候補を一定間隔に配置して順次探索)に比べて最小値/最大値近傍に至る回数を減らせますので、ブラックボックス最適化が必要になった場合に試してみる価値があります。ただし、ブラックボックス関数の探索である以上、最小/最大に至ったかどうか原理的にわかりません。実験予算が決まっていて泣いても笑っても一定の回数で打ち切るのであればそもそも判断の余地はありませんが、そうでなければ何か理屈をつけて打ち切らなければなりません。一般的には図13のようなグラフを見ながら主観で判断することになりますが、情報理論の観点から客観的な判断基準を計算する研究もありますので(※15)、興味ある方はフォローしてみてください。
(※15):「能動学習:問題設定と最近の話題」日野英逸著、日本統計学会誌 第50巻 第2号pp.317-342(2021年)
https://www.jstage.jst.go.jp/article/jjssj/50/2/50_317/_pdf
ベイズ最適化ツールの紹介 … 試作版あります
開発の目的 … Excelのような使い心地でベイズ最適化を利用できる
ちょっとしたPythonのコーディングでベイズ最適化の動作を確認できましたが、材料開発の現場にいる研究者やエンジニアにとって、ベイズ最適化に興味があってもプログラミングがハードルになっている場合があります。そこで、三井情報ではExcelのような使い心地でベイズ最適化の実行と可視化までをカバーするwebアプリケーションを開発し、2022年3月に試作版をリリースしました(※16)。材料開発研究の第一人者である一杉太郎(ひとすぎ・たろう)東京大学教授と中山亮(なかやま・りょう)同特任助教 との共同研究の中から生まれたもので、広く材料開発の現場で使われるようになることを目指しています。
(※16):/solution/mi.html
操作
画面は図14に示すように①説明変数設定部、②実験データ部(実験データを入力)、③実行コントロール部(ガウス過程回帰と獲得関数計算を実行)、④グラフ表示部からなっています。①はGPyOptにおける引数”domain”の設定に相当していますが、ログスケールでの探索(一定の比率で条件を振りたい場合、たとえば1、10、100、1,000など)も可能です。
- ①を設定
- ②で実験データを入力
- ③でベイズ最適化実行
- ②で次の探索値を取得
- 実験室で実験実施(※17)
- ②で実験データを入力
- ③でガウス過程回帰と獲得関数計算を実行
- 以上を繰り返し
のように一連のワークフローを実行することで、最大値/最小値を効率的に探索することができます。
(※17):自動実験装置と連動させれば、原理的には人の手を介さず自律的に最適条件を探索させることも可能です。
試作版は説明変数を2つまでに制限していますが(図14:説明変数を1つに設定、図15:説明変数を2つに設定)、製品版では3変数以上を扱えるように、それに伴って可視化機能も強化する予定です。まずは試作版を広く使っていただいて、そのフィードバックをもとにより良いものを造っていきたいと考えておりますので、是非お試しください!
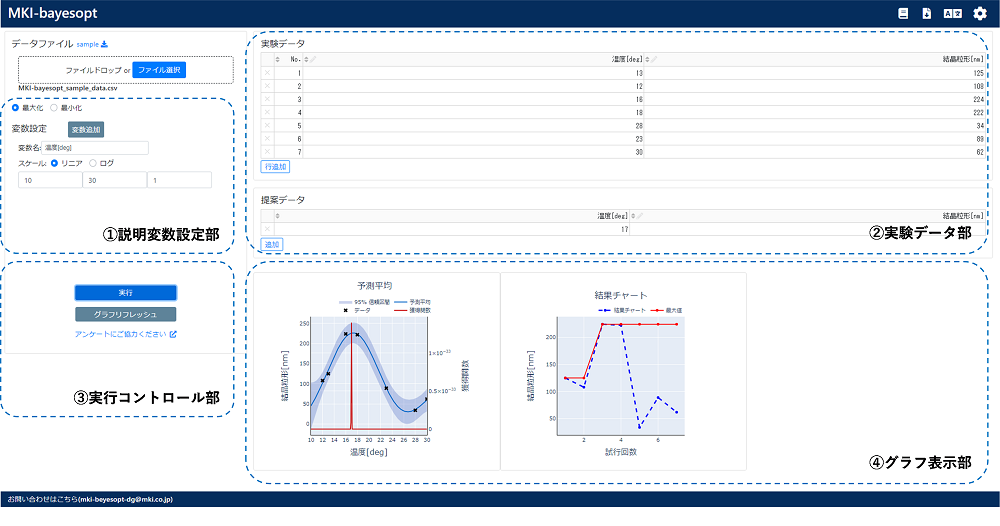
図14
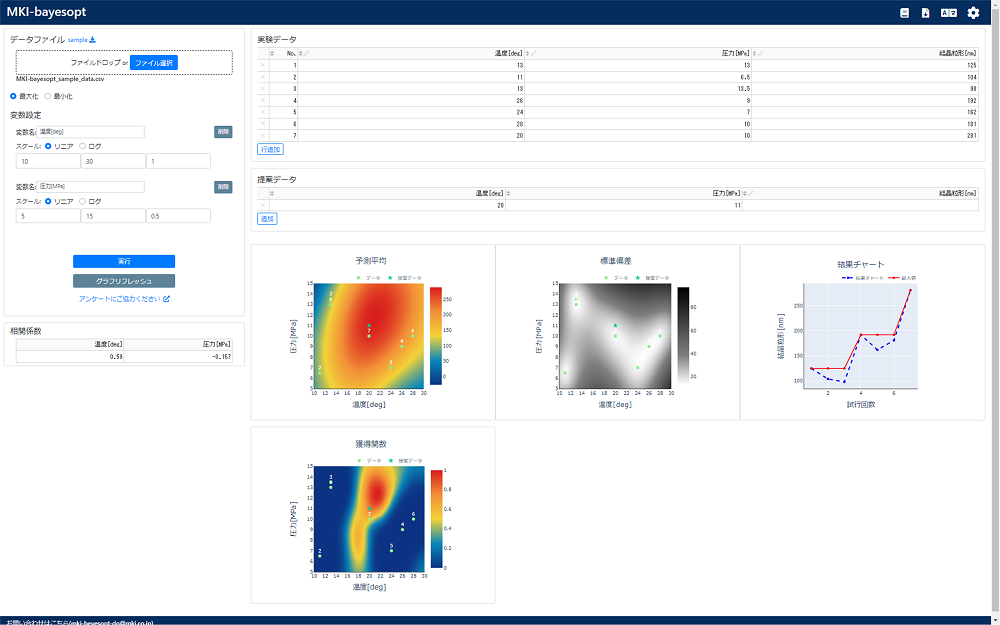
図15
関連ページ
おすすめコラム:
データサイエンスの世界へようこそ
マテリアルズ・インフォマティクスはじめました。
未来を予測すること -需要予測を例として-
関連ソリューション:
マテリアルズ・インフォマティクス
バイオインフォマティクス

中島
技術推進部
現在、シミュレーション技術の調査研究、マテリアルズ・インフォマティクス向けアプリケーションの開発、社内教育活動に従事。
コラム本文内に記載されている社名・商品名は、各社の商標または登録商標です。 本文および図表中では商標マークは明記していない場合があります。 当社の公式な発表・見解の発信は、当社ウェブサイト、プレスリリースなどで行っており、当社又は当社社員が本コラムで発信する情報は必ずしも当社の公式発表及び見解を表すものではありません。 また、本コラムのすべての内容は作成日時点でのものであり、予告なく変更される場合があります。

